最近容貌焦虑这个词很热。容貌焦虑与公序良俗、与日常生活到底什么关系?缺乏深刻的认识和分析。我们不妨用贝叶斯条件概率的计算方法,用一个实际的例子来看看,为什么人们容易产生容貌焦虑,为什么容貌焦虑如此显著而不可避免。为什么生活经验给人们的直觉是有道理的。
1. 假设有80%的人不够好看,也就是说有20%的好看,这是条件一;
2. 有20%的人会取得某种相对成功(比如容易找到好工作、好岗位),也就是说有80%的人不会取得这种成功,这是条件二。
3. 如果好看的人有90%的机会取得上述某种成功,这是条件三;
问题是:如果一个人没能取得上面的成功,那么这个人不好看的概率有多大?
这是一个典型的贝叶斯条件概率问题,如果用贝叶斯公式求解比较费劲儿,这也是阻挡了大多数人定量认清楚容貌焦虑的根本原因之一。
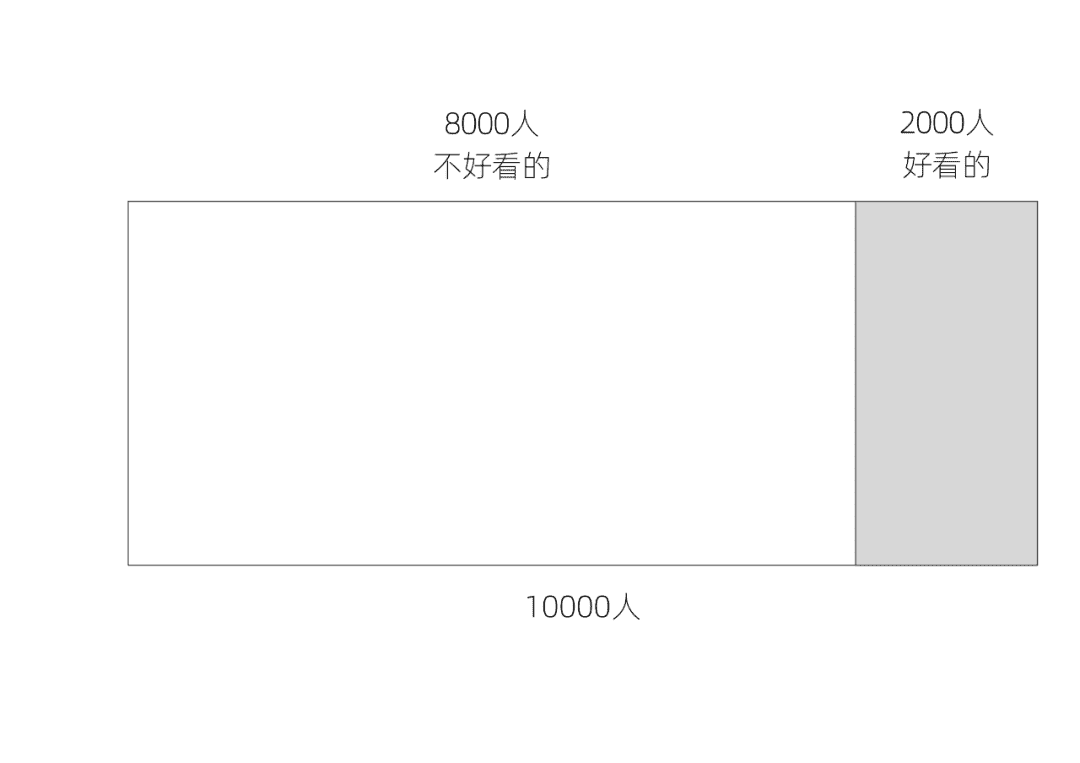
画一个图,长方形,代表10000个人,在右侧五分之四处分开,左边代表80%的8000人,右边代表20%的2000人。左边是不够好看的80%,右边是好看的20%。
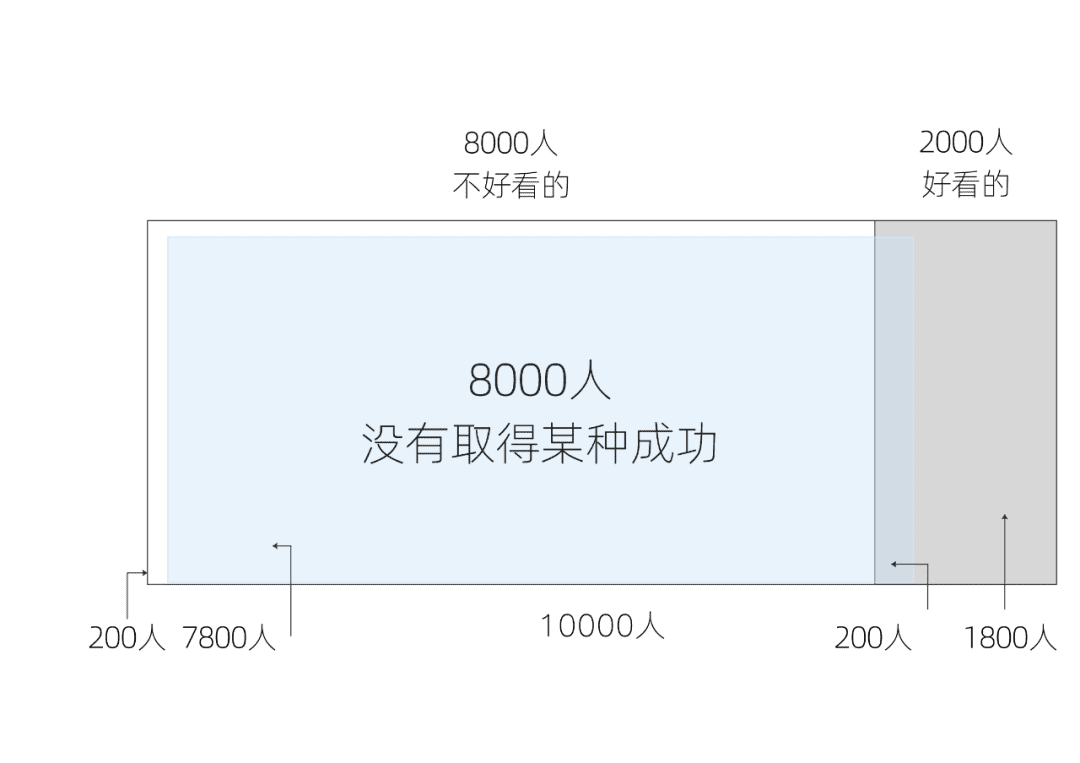
然后再画一张图,代表不能取得某种成功的8000人,如图中蓝色阴影部分所示。

如果好看的人有90%的机会能够取得这种成功,那么就是2000个好看的人里面,只有10%,也就是200人没有取得这种成功,那么剩下的7800个没有取得这种成功的人都是长得不好看的。如下图所示:
结果出来了。很直观:如果没能取得某种成功,那么与长得不好看的相关性是97.5%!
我们生活中的直觉是对的。就象我们习惯于把观察到的前后关系解释为因果关系的认知习惯,我们很容易把没有取得成功与长得不够好看关联起来。这是容貌焦虑产生的一种数学解释。
同样的算法可以适用于很多方面。其背后的数学工具是贝叶斯公式。贝叶斯算法是计算条件概率和逆概率的最重要的理论和工具,现在的大数据和人工智能有一半以上的进展是基于贝叶斯理论,甚至就是基于贝叶斯公式,利用这个公式,我们可以轻易算出这些问题:
1. 如果你的闺蜜做了水光针,那么你做水光针的概率会增加多少?
2. 如果当初你没有做双眼皮手术,那么现在你不能获得这个美好工作职位的可能性会增加多少?
3. 如果你身边的人接二连三选择了某品牌的商品或者服务,那么你为什么有极大概率也会选择这个商品或服务?
贝叶斯公式是通过指定一个先验概率然后乘以一个调整因子计算某种后验概率(条件概率)的数学思想,其原理非常简单,但是理解起来并不容易,却非常有用的一个工具。如果大家有兴趣,可以自行搜索研究,资料大把。
容貌焦虑,或者与之类似的焦虑情绪,往往都具有深刻而不被广泛认知的统计原因。统计学往往不注意因果关系,只以数据说话;人类的认知也是在省力原则的基础上运行的,习惯把相关性当成因果规律。因此,容貌焦虑是由于大量的相关事实,不断影响人们的认知和判断,最后就成了因果关系。